No século 11, Al-Biruni determinou com sucesso o raio da Terra. Ele conseguiu isso medindo a inclinação do horizonte do topo de uma colina. A partir das medições, ele foi capaz de calcular o raio da Terra.
No século 21, podemos facilmente repetir o mesmo experimento praticamente sem esforço. Só precisamos de um smartphone e uma oportunidade de observar o horizonte a partir de uma altitude elevada, como durante um voo.
Al-Biruni realizou sua medição em duas etapas.
Primeiro, ele mediu a altura de uma montanha. Ele fez duas medições do ângulo até o topo da montanha em dois locais diferentes. A partir dos resultados, ele conseguiu determinar a altura da colina.
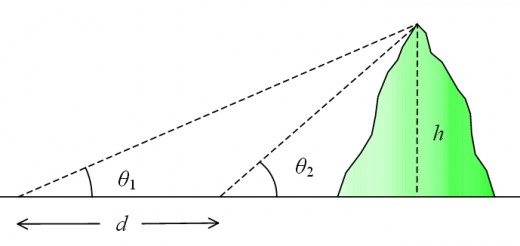
Segundo , ele subiu ao topo da montanha e mediu o mergulho do horizonte. Do ângulo do mergulho e da altura da montanha, ele calculou o raio da Terra.
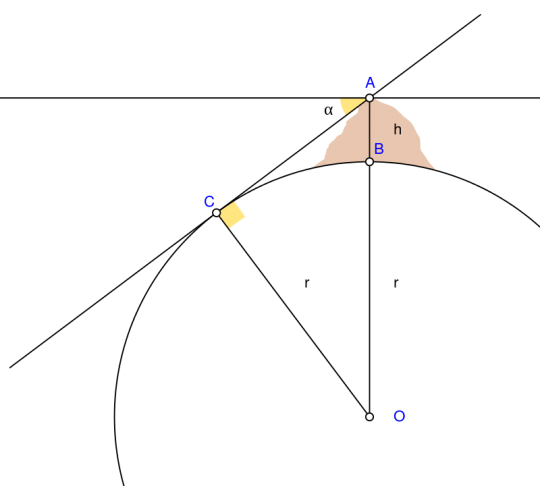
Usando a tecnologia moderna, podemos realizar a mesma medição e determinar o raio da Terra nós mesmos. Hoje em dia, praticamente todos os smartphones estão equipados com GPS que pode medir nossa altitude, com isso podemos pular o primeiro passo de Albiruni. E com os sensores do acelerômetro dentro dos nossos telefones, podemos medir a mergulho do horizonte. Usando um smartphone que usamos em qualquer lugar, podemos realizar a medição de Albiruni. Nós só precisamos estar em um local suficientemente alto e ter uma visão clara do horizonte, como durante um vôo.
Verifique se o aplicativo já está instalado antes de embarcar e, naturalmente, não se esqueça de reservar um assento na janela! Uma medida feita sobre o oceano é mais precisa. E se não acreditarmos na altitude que nossos smartphones estão nos informando, podemos sempre perguntar a um comissário de bordo ou usar o sistema de entretenimento a bordo (IFE).
Índice
Apps
Estes são alguns dos aplicativos que podemos usar para realizar a medição:
- Teodolito (IOS)
- Dioptra (Android)
- Geocam (Android)
- Surveyor Tools Free (Android)
Cálculo
Calcule usando os números na ilustração: 38805 ft * cos (3.4 graus) / (1- cos (3.4 graus)) em km = 6707.8 km
O resultado é diferente apenas cerca de 5% do valor real.
Derivação da Equação
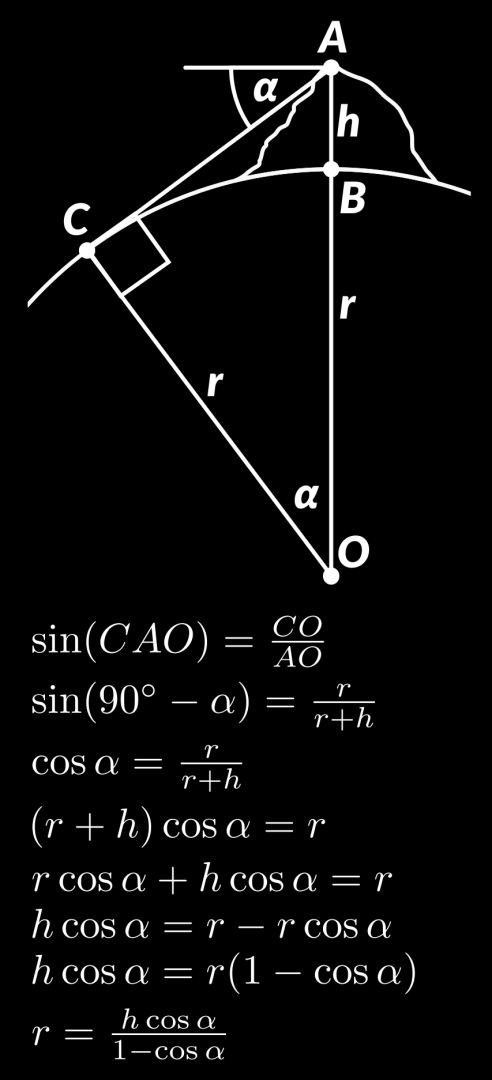
Referências
- Al-Biruni’s Classic Experiment: How to Calculate the Radius of the Earth – Owlcation
- The Empire of Reason 3/6 (Science and Islam – Episode 2 of 3) – Jim Al-Khalili – BBC
- How Al-Biruni Calculated the Circumference of the Earth Using a Mountain in the 11th Century – Flat Earth Busted


